
というわけで、今回は自然対数の底 ネイピア数e の謎に迫りたいと思います。
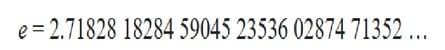
そもそも自然対数の底 ネイピア数eとはなんぞや。
そこから始めなくてはいけないのではないか…
なぜならば、わたくしも、なんのこっちゃかわかってないからであります。
あんなに高校数学で出てきたのに。なんだったら大学でもぼかすか出てきたのに…。
何かと問われれば何かわからない。それが自然対数の底 e ネイピア数です。
まずは対数から復習していきましょう。
対数とは何ぞや。
それは以下の式で表され
log 底(数字)= 対数
「この数は、ある底を何回かけたらできるのか?」を教えてくれます。
とのことです。
※AI曰く。まあ、わかるといえばわかる。
例えば、10が底の1000の対数を見ると
log₁₀(1000) = 3(10を3回かけると1000)
3が底の81の対数を見ると
log₃(81) = 4(3を4回かけると81)
2が底の1024の対数を見ると
log₂(1024) = 10(2を10回かけると1024)
要するに、xをy乗したときに、底をxとすると、xy乗の対数はy
ということですね。
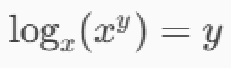
ではもうちょっと進んで、自然対数とはなんだ?
自然対数とはネイピア数eを底とした対数のことを言う。
とのことです。出てきました、ネイピア数e!
本題のネイピア数eが出てきました。
上記式の底xの部分をeとした時の対数が自然対数ということですね。
でも自然対数の底がeという定義はわかりましたが、
肝心なネイピア数eがどこから出てきたのかがよくわかりません。
というわけで一生懸命調べました。
どうもネイピア数eはいろんなところから発生してきたえみたいです。
その中で、自然対数の底として、認識されるようになってみたいで、
授業でも一体何の数字なのか、説明しにくいわけで、それもあって私の理解が追い付いていなかったみたいです。
せっかくなので、ちょっと整理してみます。
歴史に現れた順に記載すると、
①対数の研究の付録に収録されていた表
対数研究者のジョン・ネイピアさんによって以下の式を使って作られた表で、
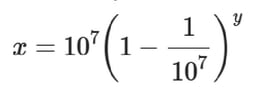
という感じで計算をしていたみたいなんですが、
ジョン・ネイピアさんは気づいていなかったようですが、上記の式を変形して、
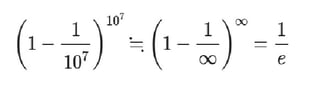
ということで、意識せず、ネイピア数eを求めていたみたいです。
なるほど。ようわからん。
②連続複利の元利合計
ヤコブ・ベルヌーイさんが計算した連続複利の計算に登場します。
連続複利とはどういうものか。
わかりやすくするために
元本:1円
年利:100%(わかりやすくするため)
複利の回数:年に何回利息をつけるか(n回)
という条件で、1円の複利を計算すると以下のような感じ
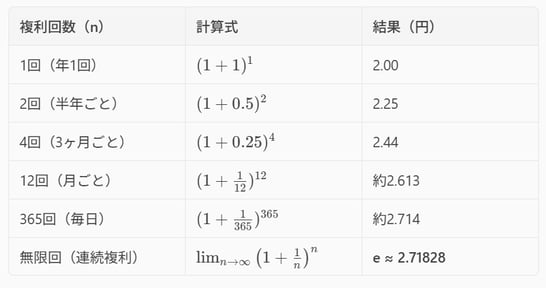
最終的に1年間を無限に分割して複利を計算すると出てくるのが、
ネイピア数eですね。
ふむ。なんとなくわかる。
③微分積分学
オイラーさんが微分積分の際に見出して、発見したとのこと。
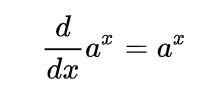
微分の上記を満たすとき a = e であることを示した、らしい
さらに
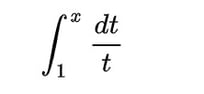
上記が対数の性質を持ち、対数として見た時の底が e でもあることを示した、らしい
うーむ。わかるようなわからんような。
微分積分に大きく関係した数ということはなんとなくわかった。
激しく理解できたとは言い難いが、とにかく自然対数の底 e ネイピア数を計算しよう。
それは次回…

