
自然対数の底 ネイピア数e をBashスクリプトで求めたい①
前回の続き
前回のブログでは、スクリプト作成まで行かず、
ネイピア数の理解で終わる…(理解したのか?)
そもそも何のブログなのか…
エンジニア関係ない…
ということでやっと本題。ネイピア数e を求めるBashスクリプトをAIに相談して作成しました。
一番わかりやすく計算できそうな連続複利から計算する。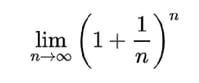
上記の式を元に計算ですね。
もちろんAIに相談する。
無限大だと当然計算できないので、
注文を出して、nの部分を引数にする。
引数をこちらで指定して、ネイピア数eを算出するスクリプトにしています。
--------------------------------------------------
#!/bin/bash
# 引数チェック
if [ -z "$1" ]; then
echo "Usage: $0 <n>"
exit 1
fi
n=$1
# bc を使って (1 + 1/n)^n を計算
e=$(echo "scale=20; (1 + 1 / $n)^$n" | bc -l)
echo "複利法によるネイピア数 e の近似 n=$n: $e"
--------------------------------------------------
簡単ですね。
なんせこれは円周率と違って、数学的にネイピア数 eを算出する計算です。
厳密に言うと引数である数字を無限大にすることで、ネイピア数 eになります。
ではそれぞれの引数nで計算。
例によって、計算時間と算出された数が以下になります。
n=10: 2.59374246010000000000
処理時間 0m0.004s
n=100: 2.70481382942152609326
処理時間 0m0.004s
n=1000: 2.71692393223589245738
処理時間 0m0.023s
n=10000: 2.71814592682522486403
処理時間 0m0.681s
n=100000: 2.71826823717448966803
処理時間 0m29.125s
n=1000000: 2.71828046931937688381
処理時間 29m10.913s
最後の1000000だと、実施したサーバーでは30分かかってしまう。
一桁少ない100000だと30秒なのに…
これ以上はやりたくないですね。もしかすると1日以上かかってしまうかもしれない。
それで1000000の精度だと、ネイピア数eに小数点以下7桁まで一致とのことです。
2.7182804 までですね。
他の方法で求めてみてもいいんですけど…
あんまり数学的には変わらなそうですね。
そもそもなんで円周率からネイピア数を発想したか、それは
円周率とネイピア数が密接に関係した
かの有名なオイラーの等式です。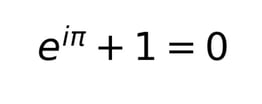
数学における最も美しい定理 らしいです。
すげえ。ていうかなんで円周率とネイピア数と虚数が絡んで等式が成立しているのか
わけがわからん。
一応、式の意味も調べてみたんですが、有名な数学者の先生が
「我々はそれを理解できないし、それがどんな意義を持っているかも分からない。だが我々はそれを証明したし、それゆえにそれが間違いのない真実であると知っている」
と言っているので、意味は分からんっぽいですね。
ちなみにですが、なぜか物理学にもよくネイピア数が登場します。
以下の通り。
①放射性崩壊の法則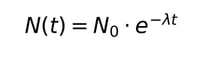
②コンデンサの放電(RC回路)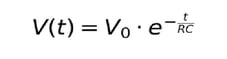
③熱伝導・拡散方程式の解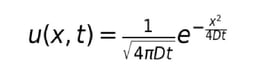
④量子力学:波動関数の表現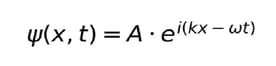
⑤ 黒体放射(プランクの法則)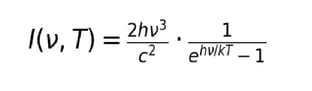
こんな感じです。すごいですねえ。
なんとなく物理の方程式によく出てくるのは微分積分が大きく関係してそうですが。
しかし、ネイピア数 eは数学の神秘ですね。
というわけでここまで。

